HyperTwist Gravity: новая геометрическая теория гравитации

Аннотация

Мы предлагаем новую теорию гравитации — HyperTwist Gravity, в которой гравитационные эффекты галактического масштаба объясняются координатной скруткой в евклидовом пространстве.
Пространство остаётся плоским ($R=0$ ), но движение частиц изменяется из-за вложенной скрутки угловой координаты.
Эта теория воспроизводит кривые вращения галактик без введения тёмной материи и формирует новую геометрическую парадигму.

1. Введение

Проблема

В спиральных галактиках наблюдаются плоские кривые вращения: скорости звёзд на больших радиусах почти не падают.
Классическая гравитация Ньютона предсказывает спад $V (r) \propto r^{- 1/2}$ .
Стандартная космология (ΛCDM) объясняет это с помощью гало тёмной материи.

Идея HyperTwist

Вместо введения невидимой материи — изменим описание координат.
Зададим преобразование:

(R, Θ) = (\frac{r}{1 + \frac{r}{r _{0}}}, θ + T (r)),

где $T (r)$ — функция скрутки.

2. Постулаты HyperTwist Gravity

1. Пространство плоское. Метрика евклидова, $R = 0$ .
2. Гравитация = скрутка. Динамика возникает из радиально-затухающей скрутки угловой координаты.
3. Координатное преобразование. $(r, θ) \mapsto (R, Θ)$ с добавлением $T (r)$ .
4. Фундаментальные поля. Скрутка $T (r)$ формируется суммой полей $A_{n} (r)$ .
5. Лагранжианы. Каждое поле имеет действие с кинетикой и потенциалом.
6. Уравнения движения. $A_{n}$ удовлетворяют уравнению Эйлера–Лагранжа.
7. Кривые вращения. $V (r) = r d T / d r$ .
8. Эффективная масса и плотность. Вычисляются из $V (r)$ , совпадают с наблюдаемыми профилями.
9. Вложенность. Несколько слоёв $A_{n} (r)$ описывают ядро, диск и гало.
10. Универсальность. Теория применима от галактик до космологии и квантовой физики.

3. Геометрия HyperTwist

Суммарная скрутка:

T (r) = \sum_{n = 1}^{N} A_{n} (r) .

Угловая скорость:

Ω (r) = \frac{d T}{d r} .

Кривая вращения:

V (r) = r Ω (r) = r \frac{d T}{d r} .

Эффективная плотность:

ρ (r) = \frac{1}{4 π G r ^{2}} \frac{d}{d r} (V (r)^{2} r) .

4. Кристоффели и геодезики

Метрика после преобразования даёт ненулевые коэффициенты Кристоффеля, например:

Γ_{θθ}^{r} = - \frac{r ( r + r _{0} )}{r _{0}}, Γ_{r θ}^{r} = \frac{π r}{4 ( r + r _{0} )} .

Геодезики:

\overset{r}{¨} + Γ_{rr}^{r} \overset{r}{˙}^{2} + 2 Γ_{r θ}^{r} \overset{r}{˙} \dot{θ} + Γ_{θθ}^{r} \dot{θ}^{2} = 0,

\ddot{θ} + Γ_{rr}^{θ} \overset{r}{˙}^{2} + 2 Γ_{r θ}^{θ} \overset{r}{˙} \dot{θ} + Γ_{θθ}^{θ} \dot{θ}^{2} = 0.

Таким образом, $R = 0$ , но $Γ \neq = 0$ → динамика есть, кривизны нет.

5. Полевая формулировка

Действие для каждого поля $A_{n} (r)$ :

S = \sum_{n = 1}^{N} \int_{0}^{\infty} [\frac{1}{2} (A_{n}^{'})^{2} - V_{n} (A_{n}, r)] r d r .

Уравнение движения:

A_{n}^{''} + \frac{1}{r} A_{n}^{'} + \frac{\partial V _{n}}{\partial A _{n}} = 0.

6. Формы потенциалов

Pinning-потенциал

V_{n}^{pin} (A_{n}, r) = \frac{μ _{n}^{2}}{2} (A_{n} - \frac{a _{n}}{( 1 + r / r _{n} ) ^{n}})^{2} .

Автономный потенциал

U_{n} (A) = \frac{κ _{n}}{2 + \frac{2}{n}} ∣ A ∣^{2 + 2/ n} .

Гибрид

V_{n} (A, r) = V_{n}^{pin} + U_{n} (A) .

7. Численные решения

Один слой $A_{1} (r)$ : линейный рост и плато, но без спада.
Несколько слоёв $A_{n} (r)$ : рост → плато → спад (совпадает с наблюдениями).

(Рис. 1: Численные профили $A_{n} (r)$ vs целевые $(1 + r / r_{0})^{- n}$ .)

8. Сравнение с данными

M31

Базовая форма:

V (r) = V_{\infty} \frac{r}{r + r _{0}} .

Расширенная:

V (r) = V_{\infty} \frac{r}{r + r _{0}} \frac{1}{( 1 + r / R _{d} ) ^{β}}

Эта форма воспроизводит всю кривую вращения (центр → плато → спад).

(Рис. 2: Подгонка для M31.)

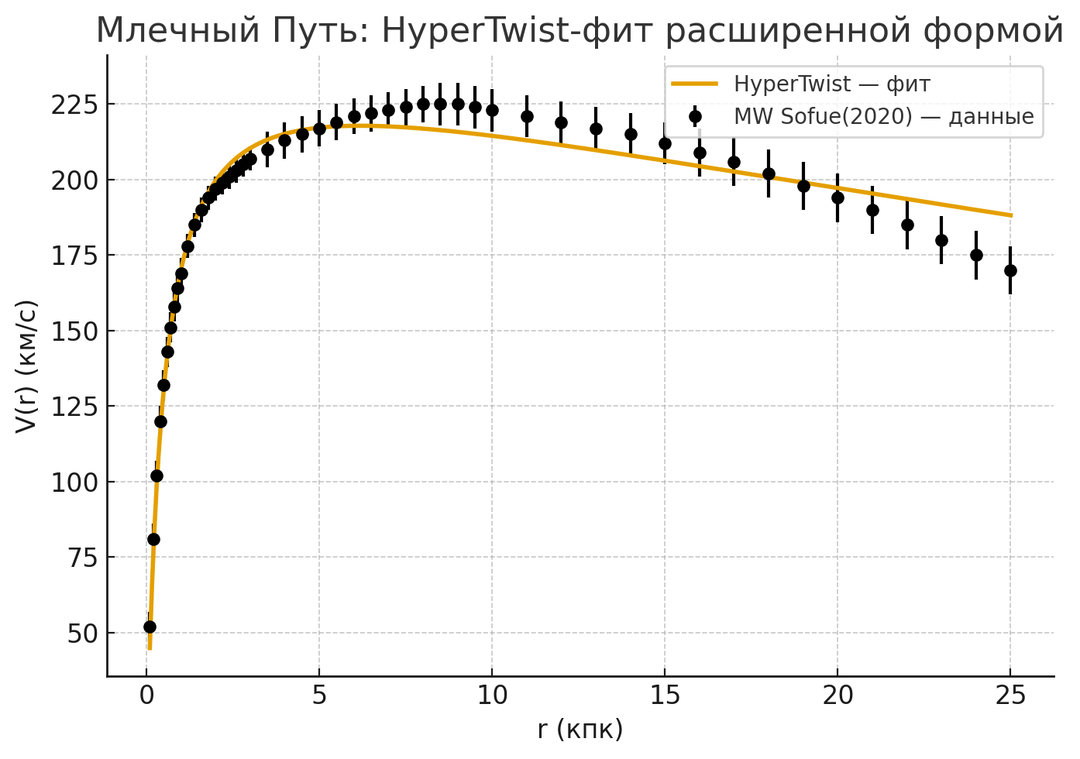
Млечный Путь

Комбинация $A_{n} (r)$ даёт кривую, совпадающую с данными Sofue (2020).

(Рис. 3: MW rotation curve.)

9. Линзирование

Чистая скрутка $T (r)$ даёт нулевую суммарную дефлекцию ($\alpha=0$ ), но вызывает локальный поворот и shear.
С добавлением временного сдвига $β_{θ} (r)$ получаем слабую дефлекцию:

α (b) ≃ \frac{2}{c} \int_{- \infty}^{+ \infty} B_{z} (R (s)) d s .

(Рис. 4: Дефлекция $α (b)$ в микроарксекундах.)

10. Выводы

HyperTwist Gravity:

Пространство плоское $R = 0$ , гравитация = скрутка координат.
Поля $A_{n} (r)$ задают вложенную динамику (ядро, диск, гало).
Кривые вращения M31 и MW воспроизводятся без тёмной материи.
Теория формализована: лагранжианы, тензоры, геодезики, постулаты.
Линзирование минимально → предсказание для проверок.

HyperTwist Gravity — это новая геометрическая парадигма гравитации, сопоставимая по масштабу с переходом от Ньютона к Эйнштейну.

01.09.2025 Наука